Du décimal au binaire.
Déterminer l'écriture binaire des entiers suivants (donnés par leur écriture en base dix) par des divisions en cascade.
- n1= 17
- n2=25
n1= 17
| quotient dans la division par 2 | reste dans la division par 2 | Division |
|---|---|---|
| 8 | 1 | 17 = 2⨯ 8+ 1 |
| 4 | 0 | 8 = 2⨯ 4 +0 |
| 2 | 0 | 4 = 2⨯ 2+0 |
| 1 | 0 | 2 = 2⨯ 1+0 |
| 0 | 1 | 1 = 2⨯ 0 + 1 |
n2= 25
| quotient dans la division par 2 | reste dans la division par 2 | Division |
| 12 | 1 | 25 = 2⨯ 12+ 1 |
| 6 | 0 | 12 = 2⨯ 6+ 0 |
| 3 | 0 | 6 = 2⨯ 3+ 0 |
| 1 | 1 | 3 = 2⨯ 1+ 1 |
| 0 | 1 | 1 = 2⨯ 0+ 1 |
Avec JavaScript
Avec l'ardoise JavaScript du logiciel Firefox et la fonction toString() présentée dans la page de cours, retrouvez les écritures binaires des deux entiers 17 et 25 de l'exercice précédent.
Voici ce que l'on peut obtenir :
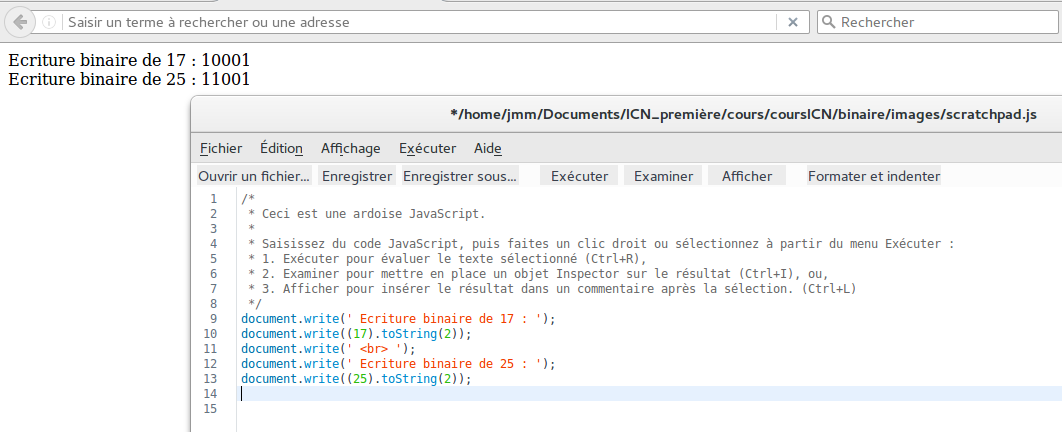
Le code document.write( '<br>' ); a permis d'aller à la ligne.
Avec JavaScript, bis
Avec la console JavaScript du logiciel Firefox et la fonction toString() présentée dans la page de cours, retrouvez les écritures binaires des deux entiers 17 et 25 de l'exercice précédent.
Voici ce que l'on peut obtenir :
De la base 10 à la base 16.
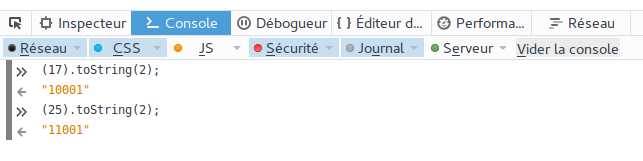
Le principe des divisions en cascade s'applique à toutes les bases.
On peut ainsi déterminer l'écriture hexadécimale (écriture en base 16) d'un entier.
Déterminer l'écriture hexadécimale des entiers suivants (ils sont donnés en base 10) à l'aide du principe de divisions en cascade.
- U = 17
- V = 184
- S = 3526
Entier U = 17
La division en cascade donne :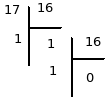 
On a donc U = 11hexadécimal.
Entier V = 184
La division en cascade donne :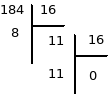 
On a donc V = b8hexadécimal (rappelons que bhexadécimal = 11décimal)
Entier S = 3526
La division en cascade donne :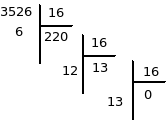 
On a donc S = dc6hexadécimal.